Cách tính phần trăm
Phần trăm là gì?
Phần trăm là một cách biểu diễn một số dưới dạng một phần của 100. Ký hiệu của phần trăm là %. Ví dụ: 50% có nghĩa là 50 phần trăm, hoặc 50 phần trên 100 phần.
Tại sao chúng ta sử dụng phần trăm?
Dễ so sánh: Phần trăm giúp chúng ta so sánh các số liệu một cách dễ dàng, dù chúng có đơn vị đo khác nhau.
Minh họa rõ ràng: Phần trăm giúp chúng ta hình dung rõ hơn về tỉ lệ, phần đóng góp của một phần so với tổng thể.
Ứng dụng rộng rãi: Phần trăm được sử dụng trong nhiều lĩnh vực khác nhau như kinh tế, tài chính, thống kê, khoa học xã hội...
Ứng dụng của phần trăm trong thực tiễn
Kinh tế: Tính lãi suất ngân hàng, giảm giá, tăng trưởng kinh tế, tỷ lệ lạm phát...
Thống kê: Tính tỷ lệ người dân ở các độ tuổi, tỷ lệ thất nghiệp, tỷ lệ tội phạm...
Khoa học tự nhiên: Tính nồng độ dung dịch, hiệu suất phản ứng hóa học...
Cuộc sống hàng ngày: Tính tip, chia tiền, tính giá trị dinh dưỡng trong thực phẩm...
Ví dụ minh họa
Giảm giá: Một chiếc áo có giá gốc là 200.000 đồng, được giảm giá 20%. Vậy giá sau khi giảm là: 200.000 x (100% - 20%) = 160.000 đồng.
Lãi suất: Gửi 10.000.000 đồng vào ngân hàng với lãi suất 6%/năm. Sau 1 năm, số tiền lãi là: 10.000.000 x 6% = 600.000 đồng.
Thống kê: Trong một lớp học có 40 học sinh, trong đó có 25 học sinh nữ. Tỷ lệ học sinh nữ là: (25/40) x 100% = 62,5%.
Phần trăm là một khái niệm quan trọng trong toán học và có ứng dụng rộng rãi trong cuộc sống. Hiểu rõ về phần trăm giúp chúng ta giải quyết được nhiều bài toán thực tế và đưa ra những quyết định đúng đắn.
Các bài toán phần trămPhần trăm là một cách biểu diễn một số dưới dạng một phần của 100. Ký hiệu của phần trăm là %. Ví dụ: 50% có nghĩa là 50 phần trăm, hoặc 50 phần trên 100 phần.
Cách tính phần trăm và các công thức tính toán phần trăm cơ bản:
Tìm một phần trăm của một số:
Công thức: Số cần tìm = (Số đã biết x Phần trăm) / 100
Ví dụ: Tìm 20% của 500.
Số cần tìm = (500 x 20) / 100 = 100
Tìm một số khi biết một phần trăm của nó:
Công thức: Số đã biết = (Số cần tìm x 100) / Phần trăm
Ví dụ: 15 là 30% của số nào?
Số đã biết = (15 x 100) / 30 = 50
Tìm tỉ số phần trăm của hai số:
Công thức: Tỉ số phần trăm = (Số thứ nhất / Số thứ hai) x 100%
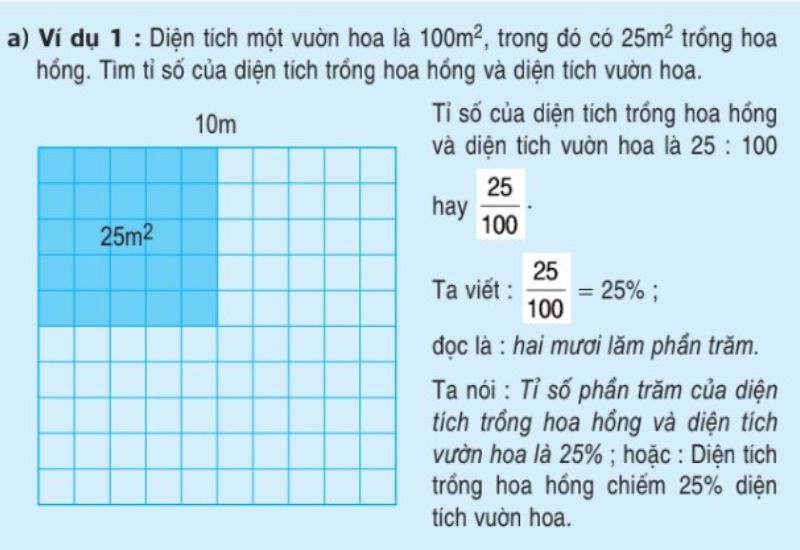
Ví dụ: Tìm tỉ số phần trăm của 25 và 100.
Tỉ số phần trăm = (25 / 100) x 100% = 25%
Một số lưu ý khi tính toán phần trăm
Đơn vị: Đảm bảo các số liệu cùng đơn vị trước khi tính toán.
Phần trăm: Phần trăm luôn được tính trên tổng thể.
Công thức: Nắm vững các công thức cơ bản để giải quyết các bài toán khác nhau.
Ví dụ thực tế
Giảm giá: Khi mua sắm, chúng ta thường gặp các chương trình giảm giá. Để tính giá sau khi giảm, ta sử dụng công thức trên.
Lãi suất: Khi gửi tiền vào ngân hàng, ta sẽ được hưởng lãi suất. Để tính số tiền lãi, ta sử dụng công thức tính lãi.
Thống kê: Trong các bảng thống kê, phần trăm được sử dụng để biểu diễn tỷ lệ, giúp chúng ta dễ dàng so sánh và phân tích dữ liệu.

Các bài toán phần trămDạng 1: Tìm một phần trăm của một số
Ví dụ: Tìm 20% của 500.
Cách giải: Số cần tìm = (500 x 20) / 100 = 100
Dạng 2: Tìm một số khi biết một phần trăm của nó
Ví dụ: 15 là 30% của số nào?
Cách giải: Số đã biết = (15 x 100) / 30 = 50
Dạng 3: Tìm tỉ số phần trăm của hai số
Ví dụ: Tìm tỉ số phần trăm của 25 và 100.
Cách giải: Tỉ số phần trăm = (25 / 100) x 100% = 25%
Dạng 4: Tìm giá trị tăng giảm
Ví dụ: Một chiếc áo giá 200.000 đồng, giảm giá 20%. Giá mới là: 200.000 x (100% - 20%) = 160.000 đồng.
Bài toán về tỉ lệ thức
Tỉ lệ thức là đẳng thức của hai tỉ số.
Ví dụ: a/b = c/d
Các tính chất của tỉ lệ thức:
Tính chất 1: Nếu a/b = c/d thì ad = bc.
Tính chất 2: Nếu ad = bc (với b, d khác 0) thì a/b = c/d.
Tính chất 3: Nếu a/b = c/d thì:
(a + b)/b = (c + d)/d
(a - b)/b = (c - d)/d
(a + b)/(a - b) = (c + d)/(c - d) (với a khác b, c khác d)
Bài toán điển hình:
Tìm số hạng chưa biết trong một tỉ lệ thức:
Ví dụ: Tìm x biết: x/5 = 3/15
Bài toán chia một số thành các phần tỉ lệ:
Ví dụ: Chia số 120 thành 3 phần tỉ lệ với 2, 3, 5.
Bài tập vận dụng
Lớp 5A có 30 học sinh, trong đó có 12 học sinh nữ. Tính tỉ lệ phần trăm học sinh nữ của lớp.
Một cửa hàng bán một chiếc ti vi với giá 8.000.000 đồng. Biết cửa hàng lãi 20% so với giá vốn. Tính giá vốn của chiếc ti vi đó.
Chia số 285 thành 3 phần tỉ lệ thuận với 3, 5, 7. Tìm mỗi phần.

Các bài toán phần trămBài toán liên quan đến nhiều lần tăng giảm: Ví dụ: Giá một chiếc xe máy tăng 10% so với giá gốc, sau đó lại giảm 5%. Tính giá cuối cùng của chiếc xe máy.
Bài toán liên quan đến lãi kép: Ví dụ: Một người gửi tiết kiệm 100 triệu đồng với lãi suất 6%/năm. Hỏi sau 2 năm người đó nhận được bao nhiêu tiền, biết rằng lãi hàng năm được nhập vào vốn để tính lãi cho năm sau.
Bài toán liên quan đến tỉ lệ thuận và tỉ lệ nghịch kết hợp với phần trăm: Ví dụ: Muốn lát xong một nền nhà cần 10 người làm trong 8 ngày. Nếu muốn lát xong nền nhà đó trong 5 ngày thì cần thêm bao nhiêu người nữa?
Bài toán liên quan đến phần trăm và phương trình: Ví dụ: Tìm một số biết rằng nếu giảm số đó đi 20% rồi lại tăng thêm 25% thì được số mới bằng 120.
Ví dụ bài toán:
Một cửa hàng bán một chiếc ti vi với giá 12.000.000 đồng. Biết rằng cửa hàng đã lãi 20% so với giá vốn. Sau đó, cửa hàng giảm giá 10% cho tất cả các mặt hàng nhân dịp lễ. Hỏi giá vốn của chiếc ti vi đó là bao nhiêu và giá bán của chiếc ti vi sau khi giảm giá là bao nhiêu?
Cách giải:
Gọi giá vốn của chiếc ti vi là x đồng.
Theo đề bài, ta có: x + 20%x = 12.000.000 => 1,2x = 12.000.000 => x = 10.000.000 (đồng)
Giá bán của chiếc ti vi sau khi giảm giá là: 12.000.000 x (100% - 10%) = 10.800.000 đồng.
Trên đây là một số thông tin về cách tính phần trăm và các dạng toán cơ bản. Hi vọng các bạn sẽ có cho mình thông tin hữu ích.