Công thức cấp số cộng
Định nghĩa cấp số cộng
Cấp số cộng là một dãy số mà trong đó, kể từ số hạng thứ hai trở đi, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi. Số không đổi này gọi là công sai và thường được kí hiệu là d.
Ví dụ: Dãy số 2, 5, 8, 11, ... là một cấp số cộng với công sai d = 3.
Tính chất của cấp số cộng
Tính chất trung bình cộng: Mỗi số hạng của cấp số cộng (trừ số đầu và số cuối nếu dãy số hữu hạn) đều bằng trung bình cộng của hai số hạng đứng kề nó.
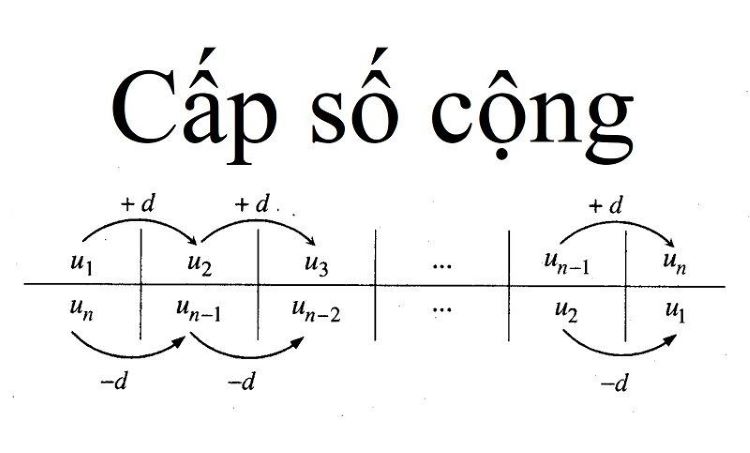
Cấp số cộng là gì? Định nghĩa và tính chấtCông thức cấp số cộng tổng quát
Số hạng tổng quát:
uₙ = u₁ + (n - 1)d Trong đó:
uₙ: Số hạng thứ n
u₁: Số hạng đầu tiên
n: Vị trí của số hạng
d: Công sai
Công thức cấp số cộng tổng n số hạng đầu:
Sₙ = [2u₁ + (n - 1)d]n / 2 Trong đó:
Sₙ: Tổng n số hạng đầu tiên
Ví dụ minh họa
Cho cấp số cộng (uₙ) có u₁ = 2 và công sai d = 3.
Tìm số hạng thứ 5:
u₅ = u₁ + (5 - 1)d = 2 + 4*3 = 14
Tính tổng 10 số hạng đầu:
S₁₀ = [2*2 + (10 - 1)*3]*10 / 2 = 165
Bài tập vận dụng
Cho cấp số cộng (uₙ) có u₃ = 7 và d = 2. Tìm u₁ và u₁₀.
Tính tổng 20 số hạng đầu của cấp số cộng có u₁ = -5 và d = 3.
Lưu ý:
Công sai d: Có thể dương, âm hoặc bằng 0.
Nếu d > 0: Dãy số tăng.
Nếu d < 0: Dãy số giảm.
Nếu d = 0: Dãy số không đổi (tất cả các số hạng bằng nhau).

Công thức tổng quát cấp số cộngBài toán tìm công sai và công bội: Cho một dãy số, biết rằng một số phần tử của dãy tạo thành cấp số cộng, một số phần tử khác tạo thành cấp số nhân. Yêu cầu tìm công sai của cấp số cộng và công bội của cấp số nhân.
Bài toán liên hệ giữa các số hạng: Cho một số điều kiện liên quan đến các số hạng của cấp số cộng và cấp số nhân, yêu cầu tìm giá trị của một số hạng hoặc chứng minh một đẳng thức nào đó.
Bài toán cực trị: Tìm giá trị lớn nhất, nhỏ nhất của một biểu thức liên quan đến các số hạng của cấp số cộng và cấp số nhân.
Bài toán ứng dụng: Áp dụng kiến thức về cấp số cộng và cấp số nhân vào các bài toán thực tế liên quan đến tài chính, vật lý, sinh học…
Bài toán kinh tế: Một người gửi tiết kiệm vào ngân hàng với số tiền ban đầu là 100 triệu đồng. Biết lãi suất hàng năm là 6% và lãi suất được nhập vào vốn hàng tháng. Tính số tiền người đó có sau 2 năm.
Bài toán vật lý: Một vật chuyển động thẳng đều với vận tốc ban đầu là 5m/s và gia tốc là 2m/s². Tính quãng đường vật đi được sau 10 giây.
Ví dụ:
Bài toán 1: Cho ba số dương a, b, c theo thứ tự lập thành cấp số cộng. Đồng thời, các số 1/a, 1/b, 1/c lập thành cấp số nhân. Tìm giá trị của biểu thức P = a² + b² + c².
Bài toán 2: Cho dãy số (uₙ) xác định bởi:
u₁ = 1
uₙ₊₁ = 2uₙ + 3ⁿ (n ≥ 1) Chứng minh rằng uₙ không là cấp số cộng cũng không là cấp số nhân. Tuy nhiên, tìm một cấp số cộng (vₙ) và một cấp số nhân (wₙ) sao cho uₙ = vₙ + wₙ với mọi n ≥ 1.
Để giải quyết các bài toán này, bạn cần
Nắm vững công thức: Cả công thức của cấp số cộng và cấp số nhân.
Phân tích bài toán: Xác định rõ các yếu tố đã biết và chưa biết, từ đó xây dựng các phương trình hoặc bất phương trình.
Sử dụng các tính chất: Áp dụng các tính chất của cấp số cộng và cấp số nhân để giải quyết bài toán.
Kết hợp các phương pháp: Có thể kết hợp phương pháp đặt ẩn phụ, phương pháp hệ phương trình để giải quyết bài toán.
Nắm vững cấp số cộng thông qua nhiều bài tập thực tếCấp số cộng là một khái niệm quan trọng trong toán học, không chỉ xuất hiện trong các bài toán lý thuyết mà còn được ứng dụng rộng rãi trong thực tế.
Ứng dụng trong toán học
Giải các bài toán liên quan đến dãy số: Tìm số hạng tổng quát, tính tổng, tìm vị trí của một số hạng,...
Xây dựng các dãy số mới: Tạo ra các dãy số có tính chất đặc biệt dựa trên cấp số cộng.
Chứng minh các tính chất toán học: Sử dụng cấp số cộng để chứng minh các định lý, bất đẳng thức.
Liên hệ với các khái niệm khác: Cấp số cộng có mối liên hệ chặt chẽ với cấp số nhân, hàm số, hình học,...
Ứng dụng trong thực tế
Kinh tế:
Tính lãi suất đơn giản: Số tiền lãi mỗi kỳ là như nhau, tạo thành cấp số cộng.
Tính giá trị của tài sản cố định sau một thời gian: Giảm dần theo một cấp số cộng (khấu hao tuyến tính).
Dự báo doanh thu, lợi nhuận trong tương lai dựa trên xu hướng tăng trưởng.
Vật lý:
Mô hình hóa chuyển động thẳng đều: Vận tốc tăng đều theo thời gian.
Tính quãng đường đi được của vật chuyển động thẳng đều.
Mô hình hóa các hiện tượng dao động điều hòa.
Sinh học:
Mô hình hóa sự tăng trưởng của một quần thể sinh vật trong điều kiện lý tưởng.
Mô hình hóa sự phân chia tế bào.
Kỹ thuật:
Tính toán các thông số kỹ thuật trong các thiết bị, máy móc.
Xây dựng các mô hình toán học để mô phỏng các quá trình sản xuất.
Cuộc sống hàng ngày:
Tính số bậc thang của một tòa nhà, số ghế trên một hàng ghế trong rạp chiếu phim.
Lập kế hoạch tiết kiệm tiền.
Trên đây là một số thông tin về định nghĩa, tính chất và công thức cấp số cộng. Hi vọng các bạn đã có cho mình thông tin hữu ích.