Đường trung tuyến là gì
Đường trung tuyến trong tam giác là một đoạn thẳng nối từ 1 trong 3 đỉnh của tam giác tới trung điểm của cạnh đối diện với đỉnh đó. Mỗi tam giác đều có 3 đường trung tuyến.
Đối với tam giác cân và tam giác đều, mỗi đường trung tuyến của tam giác chia đôi các góc ở đỉnh với hai cạnh kề có độ dài bằng nhau.
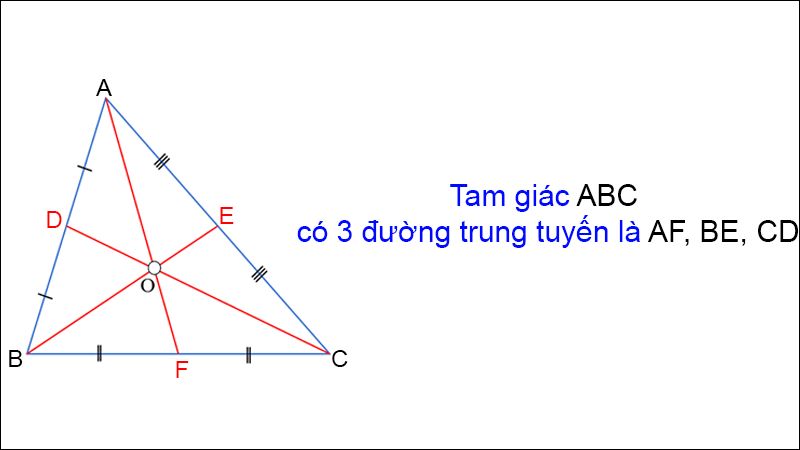
Một tam giác có 3 đường trung tuyếnSau khi tìm hiểu Đường trung tuyến là gì thì tính chất của đường trung tuyến là điều bạn cần lưu ý. Cụ thể:
Ba đường trung tuyến của một tam giác luôn gặp nhau tại một điểm duy nhất, gọi là trọng tâm của tam giác. Đặc biệt, khoảng cách từ trọng tâm đến một đỉnh của tam giác luôn bằng 2/3 độ dài của đường trung tuyến đi qua đỉnh đó.
Tam giác vuông là một trường hợp đặc biệt của tam giác, có một góc vuông 90°. Hai cạnh tạo thành góc vuông luôn vuông góc với nhau. Vì vậy, đường trung tuyến trong tam giác vuông cũng có những đặc điểm riêng biệt, phù hợp với tính chất của đường trung tuyến trong mọi tam giác. Đặc biệt, trong tam giác vuông, đường trung tuyến ứng với cạnh huyền sẽ có độ dài bằng một nửa chiều dài của cạnh huyền.
Mỗi đường trung tuyến trong tam giác đều chia diện tích tam giác thành hai phần đều nhau. Khi kết hợp cả ba trung tuyến, tam giác sẽ được chia thành ba tam giác nhỏ có diện tích bằng nhau
Đường trung tuyến trong tam giác cân
Đối với tam giác cân, đường trung tuyến từ đỉnh đến cạnh đáy sẽ vuông góc với cạnh đáy, đồng thời chia tam giác thành hai tam giác vuông đều có diện tích và hình dạng giống hệt nhau.
Đường trung tuyến trong tam giác đều
Trong tam giác đều, ba đường trung tuyến không chỉ gặp nhau tại trọng tâm mà còn chia tam giác thành sáu tam giác nhỏ có diện tích hoàn toàn bằng nhau. Thêm vào đó, mỗi đường thẳng nối từ một đỉnh đến trọng tâm của tam giác đều sẽ chia tam giác thành hai phần có diện tích bằng nhau.
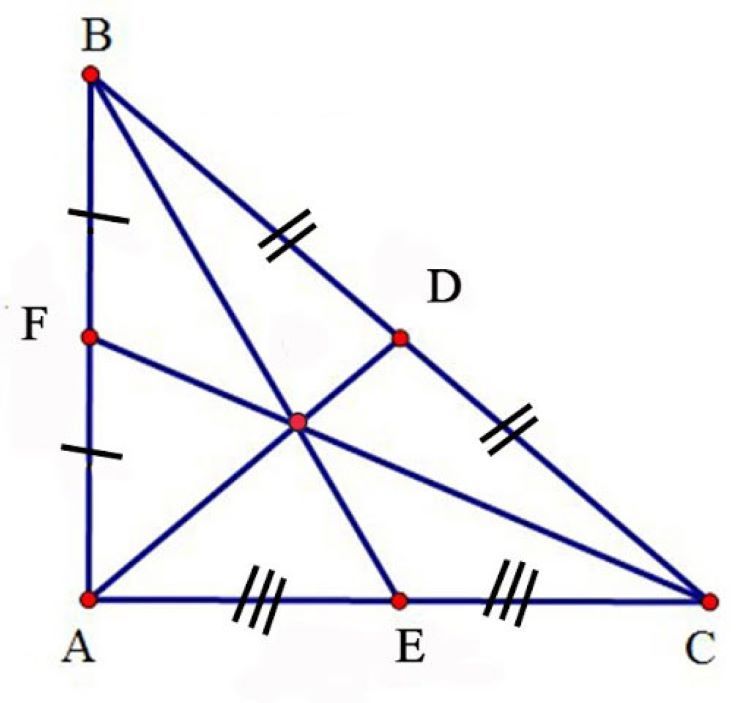
3 đường trung tuyến giao nhau tại 1 điểm, gọi là trọng tâm
- Định lý 1: Ba đường trung tuyến của một tam giác luôn đồng quy tại một điểm, và điểm này gọi là trọng tâm của tam giác.
- Định lý 2: Mỗi đường trung tuyến trong tam giác chia tam giác thành hai phần có diện tích bằng nhau. Hơn nữa, ba đường trung tuyến của tam giác cùng chia tam giác thành sáu tam giác nhỏ có diện tích hoàn toàn đồng đều.
- Định lý 3: Về vị trí của trọng tâm, nó cách mỗi đỉnh của tam giác một khoảng cách bằng 2/3 độ dài của đường trung tuyến đi qua đỉnh đó.
Ngoài lý thuyết Đường trung tuyến là gì thì công thức tính độ dài đường trung tuyến có tính ứng dụng cao. Độ dài đường trung tuyến của một tam giác sẽ được tính thông qua độ dài các 3 của tam giác, dựa theo định lý apollonnius.
Công thức tính như sau:
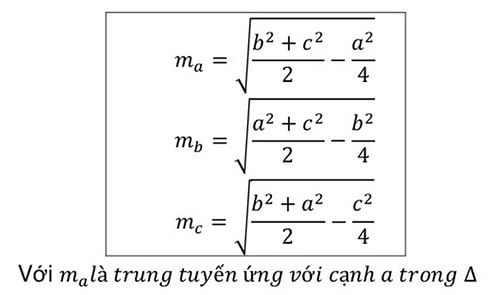
Công thức tính độ dài đường trung tuyếnTrong đó: a, b, c lần lượt là 3 cạnh của tam giác
ma, mb, mc là 3 đường trung tuyến của tam giác
Bài tập tính toán
Bài 1:
Trong tam giác ABC, M là trung điểm của cạnh BC. Tính độ dài đoạn AM nếu biết rằng AB = 6 cm, AC = 8 cm và BC = 10 cm.
Hướng dẫn:
Áp dụng định lý "Định lý trung tuyến" trong tam giác, ta có:
AM²= (2AB²+2AC² -BC²)/ 4= (2.6²+ 2.8²-10²)/4= 25
=> AM= 5
Bài 2: Trong tam giác vuông ABC vuông tại A, chiều dài các cạnh AB = 6 cm, AC = 8 cm. Tính độ dài đoạn trung tuyến AM.
Giải
Áp dụng định lý Pythagoras để tính chiều dài cạnh BC:
BC= √(AB²+AC²)= √(6²+8²)=√100=10 cm
Áp dụng công thức định lý trung tuyến:
AM²= (2AB²+2AC² -BC²)/ 4 = (2.6²+ 2.8²-10²)/4= 25
=> AM= 5cm
Vậy Đoạn trung tuyến AM có độ dài là 5 cm.
Bài tập trắc nghiệm:
Câu 1:
Trong tam giác ABC, M là trung điểm của cạnh BC. Đoạn AM là đường trung tuyến của tam giác ABC. Tính chất nào sau đây không đúng về đường trung tuyến?
A. Đoạn trung tuyến chia tam giác thành hai tam giác có diện tích bằng nhau.
B. Đoạn trung tuyến luôn cắt nhau tại trọng tâm của tam giác.
C. Đoạn trung tuyến nối một đỉnh của tam giác với trung điểm của cạnh đối diện.
D. Đoạn trung tuyến luôn vuông góc với cạnh đối diện.
>> Đáp án: D. Đoạn trung tuyến luôn vuông góc với cạnh đối diện là sai, vì chỉ có đường cao mới vuông góc với cạnh đối diện.
Câu 2:
Trong tam giác vuông ABC với góc vuông tại A, M là trung điểm của cạnh BC. Đoạn AM có đặc điểm nào sau đây?
A. AM là đường cao của tam giác.
B. AM là đường phân giác của tam giác.
C. AM là đường trung tuyến và cũng là đường cao.
D. AM không phải là một đường đặc biệt trong tam giác vuông.
>>Đáp án: C. AM là đường trung tuyến và cũng là đường cao trong tam giác vuông.
Câu 3:
Trong tam giác ABC, nếu AM là đường trung tuyến, M là trung điểm của cạnh BC, thì:
A. AM chia tam giác thành hai tam giác vuông.
B. AM chia tam giác thành hai tam giác có diện tích bằng nhau.
C. AM cắt BC tại góc vuông.
D. AM là đường cao của tam giác ABC.
>>Đáp án: B. AM chia tam giác thành hai tam giác có diện tích bằng nhau, vì đường trung tuyến luôn chia tam giác thành hai phần có diện tích bằng nhau.
Câu 4:
Trong một tam giác đều, các đường trung tuyến có đặc điểm gì?
A. Các đường trung tuyến đồng thời là các đường cao và phân giác.
B. Các đường trung tuyến chỉ là các đoạn nối các đỉnh với trung điểm của cạnh đối diện.
C. Các đường trung tuyến cắt nhau tại một điểm ngoài tam giác.
D. Các đường trung tuyến cắt nhau tại các điểm khác nhau.
Đáp án: A. Các đường trung tuyến đồng thời là các đường cao và phân giác trong tam giác đều.
Trên đây là những thông tin chi tiết về đường trung tuyến là gì và các thông tin liên quan. Hy vọng qua những chia sẻ trên, bạn nắm được định nghĩa, tính chất và công thức tính đường trung tuyến.